UNITS OF DISTANCE AND SIZE

ASTRONOMICAL UNIT (abbrv. AU) - The astronomical unit is a convenient measure of the scale of the solar system. One astronomical unit (AU) is the average distance from the Sun to Earth. An AU is equivalent to 93 million miles, or 1.5 x 10^8 km. This term is usually used in relation to solar system objects, or bodies orbiting around other suns.

Sun - Earth System

LIGHT YEAR (abbrv. ly) - A light year is a way of measuring distance not time. One light year is the distance that light can travel in one Earth year (365 days), or approximately 5,865,696,000,000 miles. Light travels 186,000 miles PER SECOND (300,000 kilometers per second). Therefore, a light second is 186,000 miles (300,000 kilometers). The closest star to Earth (Proxima Centauri, of the trinary star system Alpha Centauri) is about 24,000,000,000,000 miles, or 4.2 light years, away. That's the CLOSEST star! There are stars that are billions of times farther away than that. When you start talking about those kinds of distances, a mile or kilometer just isn't a practical unit to use because the numbers get too big. To measure really long distances, astronomers use a unit called a light year.

PARSEC (abbrv. pc) - A parsec is the distance at which 1 AU subtends and angle of 1 arcsec. Approximately 3.26 light years. Or rather, a right triangle where the length of the leg "α" (the Earth and Sun distance of 1AU) and the length of the leg "b", create a hypotenuse that is a one degree arc between "c" and "b". See previous image above of our closest star Proxima Centauri for a scale representation of a parsec.

THE EQUATORIAL COORDINATE SYSTEM

The equatorial coordinate system is what astronomers use to keep track of the positions of objects in the sky. Astronomers imagine that the Earth is surrounded by a large sphere called the celestial sphere. This is a very large imaginary sphere around the Earth with the longitude and latitude lines from the Earth projected onto it.. The Earth’s equator and the plane of the Earth’s orbit are projected onto this sphere.

The plane of the Earth’s orbit is called the ecliptic when it is projected onto the imaginary celestial sphere. Because the Earth’s axis of rotation is at a 23.5° to the plane of the Earth’s orbit, the celestial equator and the ecliptic are also at a 23.5° angle to each other.

The plane of the ecliptic and the plane of the celestial equator intersect only twice a year, once on about March 21st of each year, and once on about September 22nd. The points on the celestial sphere where this occurs are called the vernal equinox (in March) and the autumnal equinox (in September).

Equatorial or Celestial Coordinates

To denote the positions of objects in the sky, astronomers use a system based on the celestial sphere. They use two measurements, Right Ascension and Declination. Right ascension (abbreviated R.A.), is a measure of distance on the celestial sphere measured eastward along the celestial equator. It is similar to longitude and is measured in hours, minutes and seconds. Right Ascention is similar to longitude and is measured in hours, minutes and seconds eastward along the celestial equator. The distance around the celestial equator is equal to 24 hours.The right ascension of the vernal equinox is 0h 0m 0s.

Declination is similar to latitude and is measured in degrees, arcminutes and arcseconds, north or south of the celestial equator. Positive values for declination correspond to positions north of the equator, while negative values refer to positions south of the equator. The declination of the north celestial pole is 90° 0’ 0" and the south celestial pole’s declination is -90° 0’ 0". Declination at the equator is 0° 0’ 0".

The position of an object is stated with the right ascension first, then the declination. For example, the bright star Sirius’ position is R.A. 6h45m8.9s Decl. -16°42’52.1". The position of Betelgeuse is R.A. 5h55m10.3s Decl. +7°24’25.4".

While the equatorial coordinate system allows astronomers to describe the position of an object independent of position on Earth, the right ascension and declination of objects change slowly over time due to small changes in the Earth’s rotation over time due to a phenomenon called precession. So along with the R.A. and Decl. of an object, you will usually see the year or epoch those coordinates are valid for. The changes to the coordinates happen slowly enough that each epoch is 50 years long.

The Altitude - Azimuth Coordinate System

Now consider the sky, again as if it were the inside of a solid, hollow sphere. A simple, purely local, coordinate system for the sky has an axis defined by the points directly overhead and and underfoot of the observer. The overhead point is the zenith and the underfoot point is the nadir. The equator of this coordinate system is the circle that slices exactly between the zenith and nadir, corresponding to the observer's horizon. Altitude is measured in degrees above the horizon, so that the zenith is at 90º altitude, while the horizon is 0º altitude. Note that 0º altitude is not necessarily the same as your observed horizon, because the ground may not be flat, and buildings or trees might be in your sight line. It is important to measure altitude from the coordinate system's horizon, not the observed one. Azimuth is measured on a parallel to the horizon, in degrees East from North, like the markings on a compass: 90º is due East, 180º is due South, and 270º due West. If only approximate directions are required, the azimuthal direction can be specified with just cardinal directions, for example "Capella rises in the NNE". The picture below illustrates the altitude-azimuth coordinate system. On the sky, the "meridian" usually refers to the pole-to-pole line that runs overhead, through the zenith.

Because the Earth is in constant motion, the stars and other objects in the sky move from night to night, therefore the alt-azimuth coordinates one night will be different for that same object the next night. This can make finding objects on a star chart manually, difficult. With the advent of computer driven telescopes this is no longer a problem and makes non-equatorial mounted telescopes easier to build and use. This is good for astronomers since equatorial mounts are difficult and expensive to manufacture with the great precision needed to provide adequate stability. Dobsonian reflecting telescopes usually have alt-azimuth mounts. This is the most economical type of mount to buy or build for a telescope.

SIDERIAL TIME

Solar Time and Sidereal Time

Solar Time is measured by the apparent diurnal (daily) motion of the sun, and "local noon" in solar time is defined as the moment when the sun is at its highest point in the sky (exactly due south or north depending on the observer's latitude and the season). The average time taken for the sun to return to its highest point is 24 hours.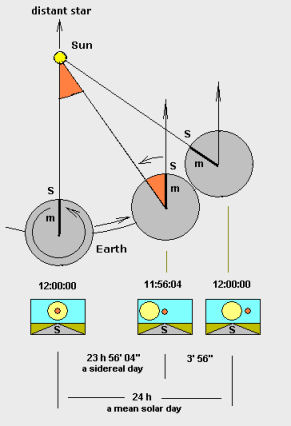

During the time needed by the Earth to complete a rotation around its axis (a Sidereal Day), the Earth moves a short distance (approximately 1°) along its orbit around the Sun. Therefore, after a sidereal day, the Earth still needs to rotate a small extra angular distance before the sun reaches its highest point (see Solar Time above). A Solar Day is, therefore, nearly 4 minutes longer than a Sidereal day. This changes where distant stars and deep sky objects can appear in the sky in relation to our sun over a period of time.

Sidereal Time is useful to astronomers because any object crosses the upper meridian when the local sidereal time is equal to the object’s right ascension (RA). Knowing when an object will near the meridian is useful because when an object is high in the sky, the distorting effect’s of the Earth’s atmosphere are minimized.